Chapter 2

Surface Brightness

The sky can be thought of as a unit sphere, which we call the celestial sphere, with objects (stars, galaxies, etc.) lying on the inside surface of this sphere, which we observe from its interior. Objects that are so distant that they appear physically smaller than the resolution of a telescope will appear point-like at a particular location on the sky, defined by polar coordinates $\theta$ and $\phi$ . The amount of energy per unit time being emitted by such a source is called its luminosity $L$ , and the fraction of $L$ that we detect with a telescope of collecting area $A$ would be

\frac{L}{4\pi d^2} \cdot A

where $d$ is the distance to the source, and $4\pi d^2$ is the area of the sphere that luminosity has been spread over (in all directions) by the time it gets to us. Defining a standard area ( $m^2$ ), we call this energy per time from the source its flux $F$

F = \frac{L}{4\pi d^2}

If we can image the object (like the Sun), then its luminosity will be spread over its surface area, and we can define the energy per time emitted per angular area of the source as its surface brightness $\Sigma = F / \Omega$ , where $\Omega$ is the angular area $(d\Omega = \sin \theta d\theta d\phi)$ . The proper unit of angular area is steradians (or square radians), although we often express angular area as square degrees, square arcminutes, or square arcseconds. Consider a star with uniform surface brightness:

Because stars are far away, we can use the small angle formula, $\tan \theta \approx \theta$ . This is generally true in astronomy, and it simplifies equations.

The angular area of the star is just the ratio of the physical area of the star $(\pi R^2_*)$ projected onto the area of a sphere centered on us with a radius of the distance to the star, so

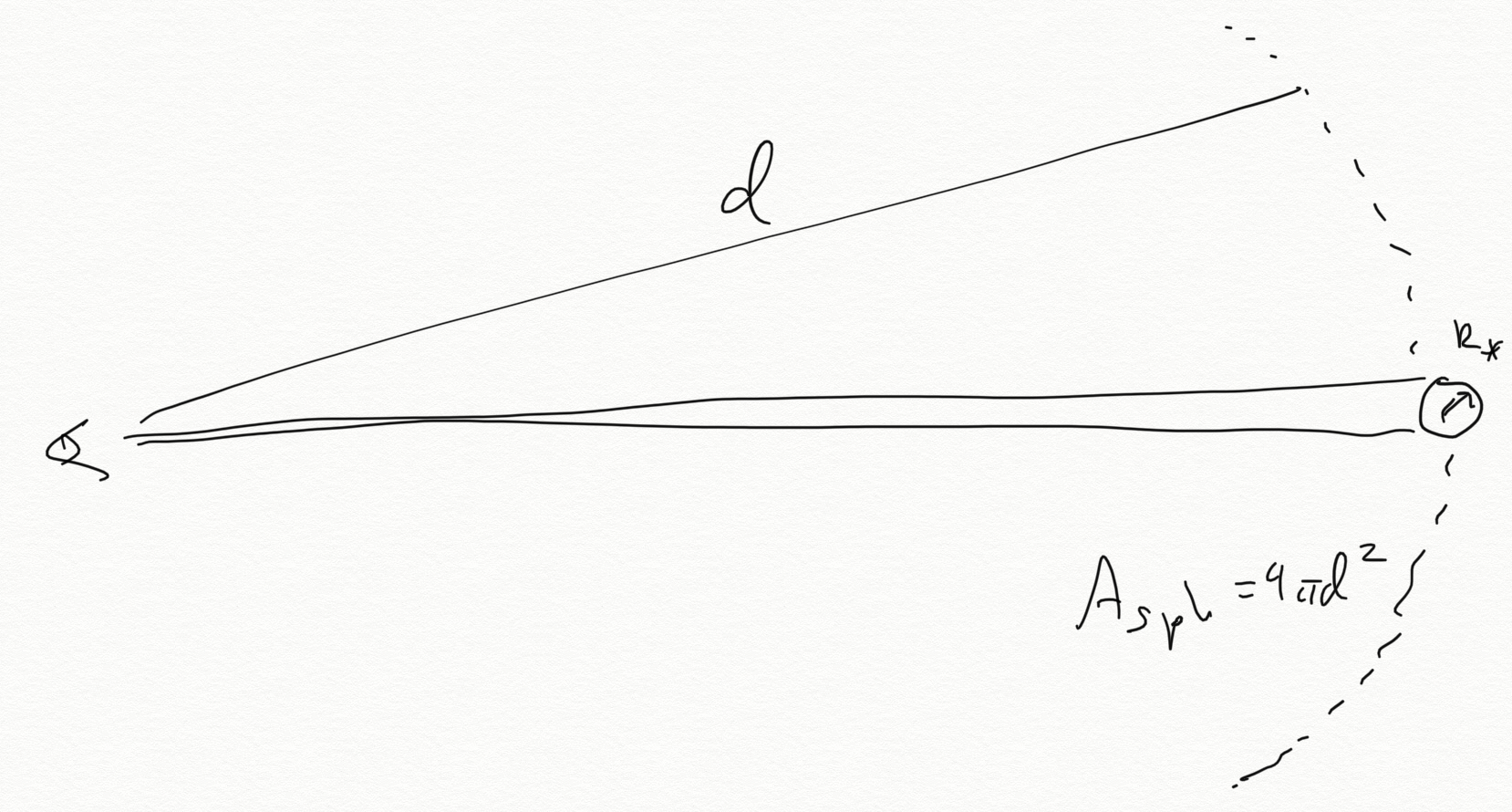
\Omega = \frac{\pi R^2_*}{4 \pi d^2} = \frac{{\rm Area~of~star~on~sphere~at~distance}~d}{\rm Total~area~of~sphere}

The surface brightness of the star is then

\Sigma_* = \frac{F}{\Omega} = \frac{L_*}{4\pi d^2} \frac{4\pi d^2}{\pi R^2_*} = \frac{L_*}{\pi R^2_*}\, ,

which is independent of the distance $d$ to the star. As we'll learn, this isn't true for galaxies that are really far away, but for galaxies in the nearby universe this holds, that surface brightness is independent of distance. Imagine a small, fixed $\Omega$ , where a star is close enough that there's only a fraction of the star's flux inside of this angle. If that star is moved farther away, the flux from the star drops $\propto d^{-2}$ , but the fraction of the flux inside $\Omega$ also increases $\propto d^2$ , so lower flux is compensated exactly by more flux entering a fixed angular area.

Hubble's Law

Redshift (or blueshift, but the former is the generic name with blueshifts being negative redshifts, just how deceleration is just negative acceleration) is the change in wavelength of light due to the Doppler shift. Just as an ambulance siren has a higher frequency (or shorter wavelength) when it is approaching you than when it leaving, the wavelength or frequency of light changes depending on whether something is moving toward/away from us:

z \equiv \frac{\lambda_{\rm obs} - \lambda_{\rm em}}{\lambda_{\rm em}} = \frac{v}{c}

where $z$ is the redshift, $\lambda_{\rm obs}$ is the observed (or shifted) wavelength, $\lambda_{\rm em}$ is the emitted (at rest) wavelength, $v$ is the line-of-sight velocity of the thing away from ( $+$ ) or towards ( $-$ ) us, and $c$ is the speed of light. The redshift $z$ is positive when things are moving away from us, which means the observed wavelength is longer ( $\lambda_{\rm obs} > \lambda_{\rm em}$ ).

Hubble's law is the empirical observation that a galaxy's velocity, determined from its redshift, is linearly proportional to its distance away from us: $v \propto d$ . This is just the equation for a straight line ( $y=Ax+b$ ), and the slope of the line or relation has been named the Hubble constant, after Edwin Hubble, who discovered this "law."

v = H_0 d = cz

The Hubble constant must have units of 1/time, but since we measure velocities in km/s and distances in Mpc, it is usually expressed as $H_0 \sim 70~{\rm km~s}^{-1}~{\rm Mpc}^{-1}$ . If you measure a galaxy's recession velocity to be 700 km/s, then you immediately know it must be ~10 Mpc away. Had the units of $H_0$ been inverse seconds, you'd need a calculator to figure out $d$ . Most units are chosen explicitly to yield answers close to 1 (i.e., $\sim 10^{\pm 3}$ ) because those are easier to remember and say out loud.

This relation implies that the universe is expanding (from any location in the universe, it appears everything is moving away from that location, simply because everything is moving away from everything else). We can define a scale factor, which compares the size of the universe at different times:

\boxed{a(t) \equiv \frac{d(t)}{d(t_0)}} = \frac{\rm distance~b/t~2~objects~in~the~past}{\rm distance~b/t~them~now}

In this course, the subscript 0 will almost always refer to the present time (i.e., $t_0$ is the current age of the universe), and other times considered will be in the past (i.e., $t<t_0$ ). This is because our observations of the universe are of past times, due to the finite speed of light. Since the universe is expanding, the distance today is always maximal (doesn't strictly have to be true, but is for realistic cosmologies) and $0 \le a \le 1$ , with $a(t_0) = 1$ .

If galaxies velocities are constant with time, then $t_0$ is just the time it has taken any galaxy to travel that far away from us at its velocity, or

t_0 = \frac{d}{v} = \frac{d}{H_0 d} = H_0^{-1} = t_H\, ,

which we call the Hubble time. (In general, $t_0 \ne t_H$ , but it is usually close to a factor of a few, so $t_H$ is a convenient unit to use when talking about the age of the universe!)

Blackbody Radiation

Blackbody radiation is the radiation emitted by a thing that absorbs all energy incident upon it (hence, it is a "black body"), and is heated up by that energy to an equilibrium temperature $T$ . Blackbodies are therefore not generally dark or black; they simply don't reflect radiation. The spectrum of light given off by such a non-reflective body in thermodynamic equilibrium is also called a Planck spectrum, and in terms of frequency it is defined as

\varepsilon(\nu) d\nu = \frac{8\pi h}{c^3} \frac{\nu^3 d\nu}{e^{h \nu / kT}-1}

which looks like this:

When $h\nu << kT$ , $e^{h\nu/kT} \rightarrow 1+h\nu/kT+\mathcal{O}([h\nu/kT]^2)$ so $\varepsilon(\nu) \propto \nu^2$ . When $h\nu >> kT$ , the exponential term becomes very large, so $\varepsilon(\nu) \propto e^{-h\nu/kT}$ . $\varepsilon(\nu)d\nu$ is the energy density of photons per unit frequency being emitted by the blackbody. Integrating over all frequencies, the total energy density is

\varepsilon = \alpha T^4\, ,~~~ \alpha = \frac{\pi^2 k^4}{15 \hbar^3 c^3}\, .

The leftover radiation from the Big Bang is now called the Cosmic Microwave Background (CMB) and now (at $t_0$ ) has a temperature $T_0 = 2.73~{\rm K}$ . The temperature was higher in the past, however. To see this, consider a volume of the universe $V$ . It will contain some amount of energy $E$ and have a pressure (recall photons also exert pressure) $P$ . Everywhere in the universe has the same $E$ and $P$ in the same volume $V$ , so any photons leaving $V$ will be replaced by similar photons entering $V$ from outside. Therefore, according to the first law of thermodynamics:

dQ = dE + PdV = 0 ~~~~~{\rm (no~net~flow~of~heat}\, Q)

We can write $E = \varepsilon V$ and $P = \frac{1}{3} \varepsilon$ , for photons, and using the integrated blackbody energy density $E = \alpha T^4 V$ and $P = \frac{\alpha}{3} T^4$ . What we want to know is how the CMB temperature changes over time, so we can put the first law in time derivative form:

\begin{array}{lll} \frac{dE}{dt} &=& \frac{d}{dt}(\varepsilon V) = \alpha \left( 4T^3\frac{dT}{dt} V + T^4\frac{dV}{dt} \right) \\ &=& -P(t) \frac{dV}{dt} = - \frac{\alpha}{3} T^4 \frac{dV}{dt} \end{array}

Equating the right sides of each line and rearranging so $T$ and $P$ fall on opposing sides of the equality, we find

\frac{1}{T}\frac{dT}{dt} = -\frac{1}{3} \frac{1}{V}\frac{dV}{dt}\, .

Now, remember the scale factor $a(t)$ from earlier? That contains all the information about how space is expanding with time, so $V(t) \propto a(t)^3$ (we could turn that into an equation using some reference distance, or we leave it as a proportionality since we don't care about the physical volume itself — in other words, it's irrelevant). Differentiating the expression for volume, we get

\frac{1}{T}\frac{dT}{dt}\propto -\frac{1}{a}\frac{da}{dt}\, .

Recognizing that $d(\ln x) = x^{-1} dx$ , the above can be rewritten as $\frac{d}{dt}(\ln T) \propto - \frac{d}{dt}(\ln a) \propto \frac{d}{dt}(\ln a^{-1})$ , or that $T \propto a^{-1}$ ! Since $T(t_0) = T_0$ and $a(t_0) = 1$ , we can now turn this proportionality into an equation:

\boxed{T(t) = T_0 a(t)^{-1}}\, .

When the universe "half" its current size, or $a(t) = 0.5$ (really when some volume today was crammed into a $\left(\frac{1}{2}\right)^3 = \frac{1}{8}$ smaller volume), the CMB's temperature was twice as hot as it is today.